Att räkna ut hypotenusan i en rätvinklig triangel är en grundläggande färdighet inom geometri.
Hypotenusan är den längsta sidan i en rätvinklig triangel och ligger alltid mittemot den räta vinkeln. Vi använder Pythagoras sats för att räkna ut hypotenusan.
Pythagoras sats säger att i en rätvinklig triangel är kvadraten på hypotenusan lika med summan av kvadraterna på de andra två sidorna.
Formeln för att räkna ut hypotenusan är:
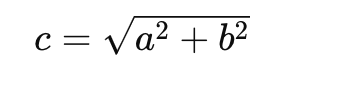
Där:
- c är hypotenusan
- a och b är de andra två sidorna
Exempel 1
Anta att vi har en rätvinklig triangel där de två kortare sidorna är 3 cm och 4 cm långa.

Så, hypotenusan är 5 cm.
Exempel 2
Anta att vi har en rätvinklig triangel där de två kortare sidorna är 5 cm och 12 cm långa.

Så, hypotenusan är 13 cm.
Exempel 3
Anta att vi har en rätvinklig triangel där de två kortare sidorna är 8 cm och 15 cm långa.

Så, hypotenusan är 17 cm.
Sammanfattning
För att räkna ut hypotenusan i en rätvinklig triangel:
1. Kvadrera de två kortare sidorna.
2. Addera dessa kvadrerade värden.
3. Ta kvadratroten ur summan.
Genom att följa dessa steg kan du enkelt räkna ut hypotenusan i vilken rätvinklig triangel som helst.




